系统如下
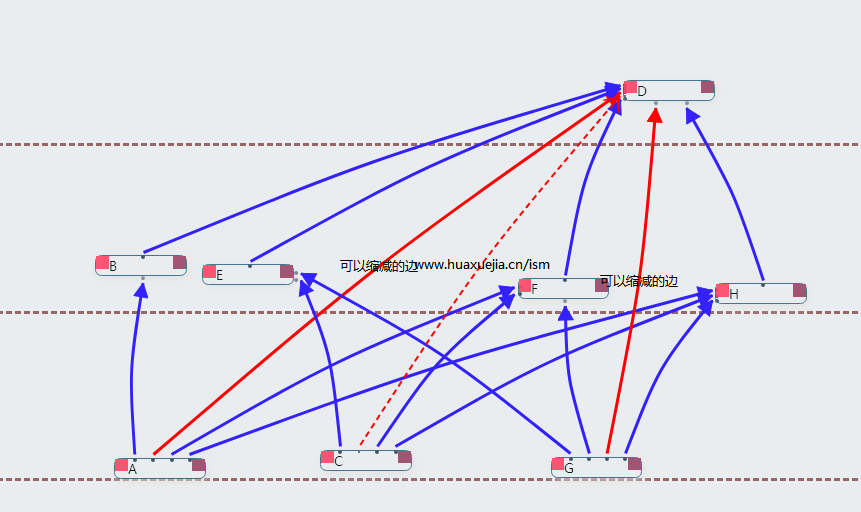
选择任何缩边的方式都得到如下缩减图$S$
$C \longrightarrow D$ 可以缩减掉 因为存在着 $C \longrightarrow E \longrightarrow D$一条路径可以覆盖其可达性。
缩点的计算有四个选项:
1、不计算
2、方式1
3、方式2
4、方式3
对于不含回路的图缩边有简单的代数形式的计算
$HS=S=R-(R-I)^2-I$
其中$R$为可达矩阵;$I$为单位矩阵,即对角线都为1的矩阵。$S$为骨架矩阵、又叫缩边矩阵、骨架阵。$HS$称为哈斯矩阵
系统如下

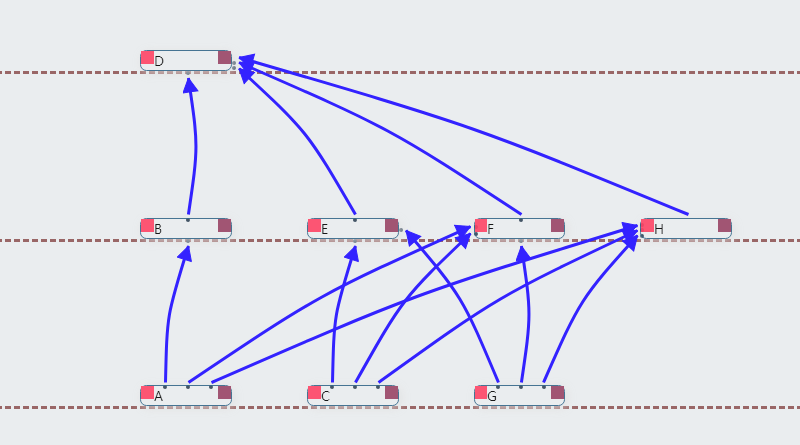
选择任何缩边的方式都得到如下缩减图$S$

$C \longrightarrow D$ 可以缩减掉 因为存在着 $C \longrightarrow E \longrightarrow D$一条路径可以覆盖其可达性。
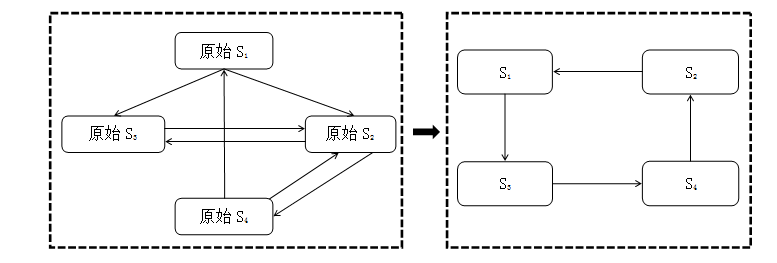
上图为菊花链的表示
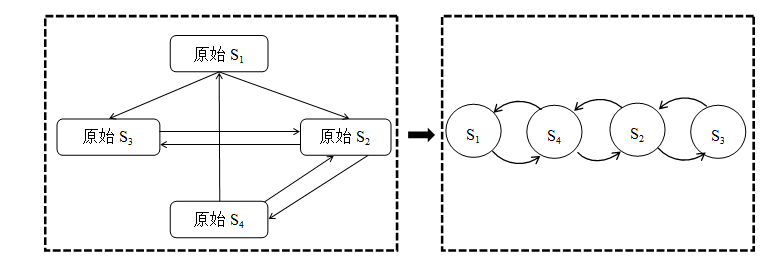
上图为套环链的表示
菊花链方式更好,因为没有那么多边。
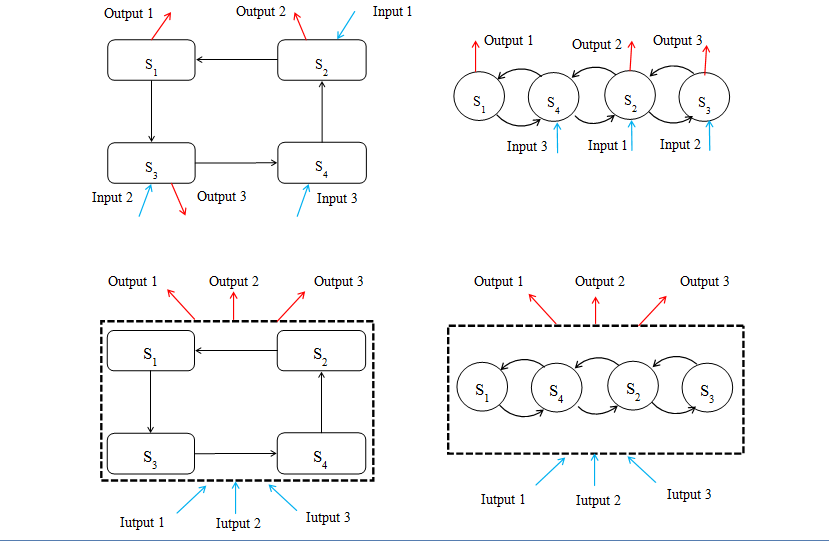
上图下面两个一个是菊花链表示形式,一个是套环的模式
总之:会绘制菊花链才算懂了ISM方法
推荐好玩的模型:扯蛋模型