大力推动哈斯图方法的人是布吕格曼 (Brüggemann)。而布吕格曼用得最多的方法叫Averaged Ranks of Partial Orders 其中的 Ranks本处翻译成等级、层级。
布吕格曼 (Brüggemann)发表的一大坨哈斯图方法的文章，大部分都是用平均层级来捣鼓的。此外他还用python捣鼓了一个东西。
有一些文章挺有意思的，那就是两篇文章看着几乎是一模一样的，但是在不同的刊物发表。
除了文章他还写了好几本书。
其中有一本书叫《partial order in environmental sciences and chemistry》，里面全部是讲偏序，这本书最有意思的是页数，总共是404，所以让人印象深刻。点击下载
此外他还写了一本 Multi-indicator Systems and Modelling in Partial Order 这本书里有讲到他的python写的东西，不过目前没有看到软件发布在哪里点击下载
现把他发表的一些文章列一下：
1、A Theoretical Concept To Rank Environmentally Significant Chemicals
3、Estimation of Averaged Ranks by a Local Partial Order Model
4、Giving Molecules an Identity. On the Interplay Between QSARs and Partial Order Ranking
5、Estimation of averaged ranks by extended local partial order models
6、Partial Order Concepts in Ranking Environmental Chemicals
7、Partial Order in Environmental Sciences and Chemistry
9、The concept of stability fields and hot spots in ranking of environmental chemicals
10、An Improved Estimation of Averaged Ranks of Partial Orders
其中最后一篇是本文讨论的重点。该文中的例子，岳立柱说布吕格曼算错了。
基本概念与定义
基于线性拓展的偏序规则的文章有不少。就布吕格曼的文章来说有好几篇。最终可操作的公式非常简单。在理解计算规则前，先要了解如下基本概念。
1、关系矩阵、原始矩阵、相乘矩阵、布尔矩阵、布尔矩阵对应的有向图表示。
这些都是解释结构模型中的基本概念，不再累述，但是基于偏序集的关系矩阵有如下特征。
A、为了跟ISM相关定义一致，该原始矩阵（关系矩阵）通常用$A$，或者用$O$来表示。
B、原始矩阵$O$中不存在回路,即对应的图为DAG。
C、通常原始矩阵$O$的对角线的值都为1，即加上了单位矩阵$I$。
2、可达矩阵，本处用$R$表示
3、哈斯矩阵$HS$就是骨架矩阵$S$，原始矩阵连乘直到不发生变化时候即为可达矩阵。
$$O^{(k-1)}≠O^{k}=O^{(k+1)}=R$$
$$HS=S=R-(R-I)^2-I$$
其中 $O：$原始矩阵 ； $I：$单位矩阵；$R：$可达矩阵；$S：$骨架矩阵；$HS：$哈斯矩阵。
4、可达集合，可达集合要素个数，上位集，上集，结果集合。
A、对于可达矩阵中的某一要素j，其可达集合记作$R_{(j)}$它又叫做上位集合，结果集合，上集代表某个要素能到达的要素。
B、对于可达矩阵中的某一要素j，可达集合要素个数$Rnums_{(j)}$它就是可达矩阵中，j行中为1的值的总数目，由于要素自身到自身总是可达因此该数目不可能小于1。
5、先行集合，先行集合要素个数，下位集，下集，原因集合、起始集合。
A、对于可达矩阵中的某一要素j，其原因集合记作$Q_{(j)}$它又叫做下位集合，原因集合，下集代表所有能能到达的j要素的集合。
B、对于可达矩阵中的某一要素j，可达集合要素个数$Qnums_{(j)}$它就是可达矩阵中，j列中为1的值的总数目，由于要素自身到自身总是可达因此该数目不可能小于1。
撇开证明部分，计算平均层级的简化公式1如下。
$$ \rho _{(j)}=\frac {(n+1) \times Rnums_{(j)} } { Rnums_{(j)} + Qnums_{(j)} }$$
$$其中： \rho _{(j)}表示第j个要素的平均层级 \quad \quad \qquad \\ n 为可达矩阵要素的数目 n+1代表的意思为，各个要素是处于 1到n+1之间的层级，也可以看成是 0到 n之间的层级浮动 $$
数据来源：An Improved Estimation of Averaged Ranks of Partial Orders 一文第405页
$$ \begin{array}{c|c|c|c|c|c|c} {ID} & Chemical & 中文名 \quad \quad & CAS NO & Carcinogenic致癌 \quad & Mutagenic致突变 \quad & Teratogenic致畸性 \quad \quad & Embryotoxic胚胎毒性 \\ \hline 1 & 1,1-dimethyl-hydrazine & 偏二甲肼 &57-14-7 &0.955 &0.762 &0.689 &0.672\\ \hline 2 & Trimethyl amine &三甲胺 &75-50-3 &0.619 &0.25 &0.25 &0.527\\ \hline 3 & Dimethylamine & 二甲胺 &124-40-3 &0.25 &0.25 &0.563 &0.25\\ \hline 4 &1,1,4,4-Tetramethyltetrazene & 1,1,4,4-四甲基-2-四氮烯 \quad & 6130-87-6 &0.894 &0.792 &0.946 &0.816\\ \hline 5 &N-Nitrosodimethyl-amine & 亚硝基二甲胺 &62-75-9 &0.98 &0.969 &0.952 &0.866\\ \hline 6 &N,N-Dimethyl formamide & 二甲基甲酰胺 &68-12-2 &0.951 &0.25 &0.614 &0.795\\ \hline 7 &Tetramethylhydrazine &四甲基联氨 &6415-12-9 &0.827 &0.539 &0.698 &0.604\\ \hline 8 &Acetaldehyde dimethyl hydrazone &乙醛二甲基腙 &7422-90-4 &0.98 &0.25 &0.25 &0.25\\ \hline 9 &Formaldehyde dimethyl hydrazone & N-甲基-N-(亚甲基氨基)甲胺 &2035-89-4 &0.683 &0.25 &0.25 &0.25\\ \hline 10 &Trimethyl hydrazine & 三甲基-肼 &1741-01-1 &0.923 &0.619 &0.811 &0.681\\ \hline 11 &Acetaldehyde &乙醛 &75-07-0 &0.628 &0.25 &0.25 &0.25\\ \hline 12 &1-Formyl 2,2-dimethylhydrazine &二甲基-肼醛 &3298-49-5 &0.897 &0.524 &0.53 &0.25\\ \hline 13 & Dimethylamino acetonitrile &(二甲氨基)乙腈 &926-64-7 &0.25 &0.25 &0.25 &0.25\\ \hline 14 &Ammonia &氨气 & 7664-41-7 &0.25 &0.25 &0.25 &0.25\\ \hline 15 &Hydrogen cyanide (b) & 氰化氢& 74-90-8 &0.25 &0.25 &0.25 &0.25\\ \hline 16 &1,3-Dimethyl-1H1,2,4-triazole & 1,3-二甲基1H1,2,4三唑& 16778-76-0 &0.25 &0.25 &0.25 &0.25\\ \hline 17 &1-Methyl-1H1,2,4-triazole &1-甲基-1,2,4-三唑 & 6086-21-1 &0.25 &0.25 &0.25 &0.25\\ \hline 18 & 1-Methyl-1Hpyrazole & N-甲基吡唑& 930-36-9 &0.25 &0.25 &0.25 &0.25\\ \hline \end{array} $$
上述数据，中文名字根据CAS号添加。
同时可以看到序号为13-18的数据完全一致，它们之间为一回路，可以看成同一个东西。
最终的结果为：
当矩阵值$f_{x1} \geqslant f_{y1} 且f_{x2} \geqslant f_{y2} 且 f_{x3} \geqslant f_{y3} {\cdots}且f_{xm} \geqslant f_{ym}$
记作：$$ \quad \quad PS_{(x)}\geqslant PS_{(y)}$$
关系矩阵获得的方式如下两种可以任选一种：
$$a_{xy}= \begin{cases} 1, PS_{(x)} {\geqslant} PS_{(y)} \\ 0, \end{cases} $$
$$a_{xy}= \begin{cases} 1, PS_{(y)} \geqslant PS_{(x)} \\ 0, \end{cases}$$
以上两种，核心在于$\geqslant$的定义。即，模糊矩阵的任意两行$x,y$行，且$x \neq y$对应的任意一个值都是大于等于关系情况下，得到关系矩阵中对应的布尔值。
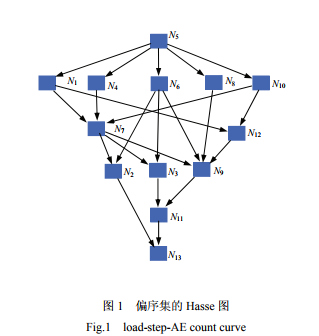
上面的哈斯图是运用原因优先的层级抽取方法得到的层级拓扑图。
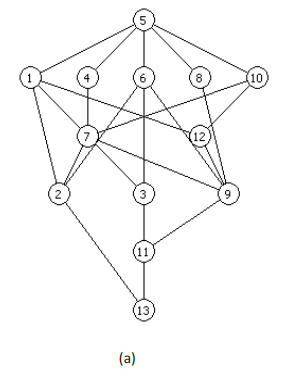
因此与原文对应，原文的图反转，并把有向边方向加上即是该图。
同时可以看到，原文的A13直观上看是错的。13要素应该接收了3条有向边，而原图看上去却只有两条边。其实就是布吕格曼的软件PyHasse不是很友好导致，它的要素不能拖动，然后11刚好居中显示。
于是有$11\Longrightarrow 13$ 把$3 \Longrightarrow 13$挡住了一半。因此直观上看该哈斯图看着是错的。
而岳立柱刚好在应用关系矩阵表示偏序集平均高度的方法一文有探讨平均层级，且刚好用到这个例子。很显然岳立柱把这个图看错了。
岳立柱在文中称:"……计算13个样本的上下集，有3个样本的计算存在错误，错误比率达 23.8%……"
事实上并不是布吕格曼算错了，或者说他的软件算错了，而是岳立柱把图看错了,或者说岳立柱算错了。岳立柱说布吕格曼算错了是说错了的。
不过布吕格曼跟岳立柱的推理跟证明都没有问题。
原始矩阵与可达矩阵有$O=R$
$$ \begin{array}{c|c|c|c|c|c|c}{M_{13 \times13}} &A1 &A2 &A3 &A4 &A5 &A6 &A7 &A8 &A9 &A10 &A11 &A12 &A13\\ \hline A1 &1 &1 &1 &0 &0 &0 &0 &0 &1 &0 &1 &1 &1\\ \hline A2 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1\\ \hline A3 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1\\ \hline A4 &0 &1 &1 &1 &0 &0 &1 &0 &1 &0 &1 &0 &1\\ \hline A5 &1 &1 &1 &1 &1 &1 &1 &1 &1 &1 &1 &1 &1\\ \hline A6 &0 &1 &1 &0 &0 &1 &0 &0 &1 &0 &1 &0 &1\\ \hline A7 &0 &1 &1 &0 &0 &0 &1 &0 &1 &0 &1 &0 &1\\ \hline A8 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &1 &0 &1\\ \hline A9 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &1 &0 &1\\ \hline A10 &0 &1 &1 &0 &0 &0 &1 &0 &1 &1 &1 &1 &1\\ \hline A11 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &1\\ \hline A12 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &1 &1 &1\\ \hline A13 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1\\ \hline \end{array} $$$$简化公式 \rho _{(j)}=\frac {(n+1) \times Rnums_{(j)} } { Rnums_{(j)} + Qnums_{(j)} }$$
$$ \begin{array}{c|c|c|c|c|c|c}{M_{13 \times3}} &可达集数量，上位数 &前因数量，下集数 &平均高度\\ \hline A1 &7 &2 &10.888888888889\\ \hline A2 &2 &7 &3.1111111111111\\ \hline A3 &2 &7 &3.1111111111111\\ \hline A4 &7 &2 &10.888888888889\\ \hline A5 &13 &1 &13\\ \hline A6 &6 &2 &10.5\\ \hline A7 &6 &4 &8.4\\ \hline A8 &4 &2 &9.3333333333333\\ \hline A9 &3 &9 &3.5\\ \hline A10 &8 &2 &11.2\\ \hline A11 &2 &10 &2.3333333333333\\ \hline A12 &4 &4 &7\\ \hline A13 &1 &13 &1\\ \hline \end{array} $$跟布吕格曼一文进行比较：
$$ \begin{array}{c|c|c|c|c|c|c}{M_{13 \times3}} &可达集数量，上位数 &前因数量，下集数 &平均高度 & 文献中中LPOM0的值\\ \hline A1 &7 &2 &10.888888888889 & \color{#F11}{10.889 }\\ \hline A2 &2 &7 &3.1111111111111 &\color{#F11}{3.111 }\\ \hline A3 &2 &7 &3.1111111111111 &\color{#F11}{3.111 }\\ \hline A4 &7 &2 &10.888888888889 & \color{#F11}{10.889 }\\ \hline A5 &13 &1 &13& \color{#F11}{13.0 }\\ \hline A6 &6 &2 &10.5 & \color{#F11}{10.5 }\\ \hline A7 &6 &4 &8.4 & \color{#F11}{8.4 }\\ \hline A8 &4 &2 &9.3333333333333 & \color{#F11}{9.333 }\\ \hline A9 &3 &9 &3.5 & \color{#F11}{3.5 }\\ \hline A10 &8 &2 &11.2 & \color{#F11}{11.2 }\\ \hline A11 &2 &10 &2.3333333333333 & \color{#F11}{2.333 }\\ \hline A12 &4 &4 &7 & \color{#F11}{7 }\\ \hline A13 &1 &13 &1 & \color{#F11}{1 }\\ \hline \end{array} $$
结论：
布吕格曼的数算对了，但是那个图是没整好的容易引起歧义，或者说那个PyHasse软件有待完善。
岳立柱说错了，是在有歧义的图上讨论，如果岳立柱重头算起，就不会武断的下结论。
抽象一点说，平均层级是一个几何空间的性质，而ISM或者哈斯图是一个拓扑空间的性质。
平均层级中的层级是拓扑空间在几何空间的一个投射。不变的是，拓扑层级是不变的。
上图是按照所谓的平均层级展示的哈斯图。其意义就是把整个系统看成一个弹簧一样的东西，往一个方向拉，拉出来的一个东西。
最新的哈斯图，没有变的东西是有向边的方向，一旦任意一条有向边的方向发生了逆转，比如出现了平的或者朝下，则说明不是算错了，就是方法本身有问题。
哈斯图上蹿形式，是最常见，它是结果优先的抽取方法。即：$T(e_i)=R(e_i)$
下跳形式的哈斯图，是原因优先的抽取方法。即：$T(e_i)=Q(e_i)$
上述方法的具体流程，可以参看 轮换法获得的层级为什么比经典的方法更好
生成式对抗网络（GAN, Generative Adversarial Networks ）是一种深度学习模型，是近年来复杂分布上无监督学习最具前景的方法之一。模型通过框架中（至少）两个模块：生成模型（Generative Model）和判别模型（Discriminative Model）的互相博弈学习产生相当好的输出。
GAN是2014年由Ian Goodfellow第一次提出， Generative Adversarial Networks（arxiv：https://arxiv.org/abs/1406.2661），是第一篇GAN的论文，从这篇开山之作开始，对抗的概念开始贯穿于机器学习领域。
阿尔法围棋（AlphaGo）是第一个击败人类职业围棋选手、第一个战胜围棋世界冠军的人工智能机器人，由谷歌（Google）旗下DeepMind公司戴密斯·哈萨比斯领衔的团队开发。
阿尔法围棋（AlphaGo）是通过两个不同神经网络“大脑”合作来改进下棋。这些“大脑”是多层神经网络，跟那些Google图片搜索引擎识别图片在结构上是相似的。它们从多层启发式二维过滤器开始，去处理围棋棋盘的定位，就像图片分类器网络处理图片一样。经过过滤，13个完全连接的神经网络层产生对它们看到的局面判断。这些层能够做分类和逻辑推理。
第一大脑：落子选择器 （Move Picker）
阿尔法围棋（AlphaGo）的第一个神经网络大脑是“监督学习的策略网络（Policy Network）” ，观察棋盘布局企图找到最佳的下一步。事实上，它预测每一个合法下一步的最佳概率，那么最前面猜测的就是那个概率最高的。这可以理解成“落子选择器”。
第二大脑：棋局评估器 （Position Evaluator）
阿尔法围棋（AlphaGo）的第二个大脑相对于落子选择器是回答另一个问题，它不是去猜测具体下一步，而是在给定棋子位置情况下，预测每一个棋手赢棋的概率。这“局面评估器”就是“价值网络（Value Network）”，通过整体局面判断来辅助落子选择器。这个判断仅仅是大概的，但对于阅读速度提高很有帮助。通过分析归类潜在的未来局面的“好”与“坏”，阿尔法围棋能够决定是否通过特殊变种去深入阅读。如果局面评估器说这个特殊变种不行，那么AI就跳过阅读。 这些网络通过反复训练来检查结果，再去校对调整参数，去让下次执行更好。这个处理器有大量的随机性元素，所以人们是不可能精确知道网络是如何“思考”的，但更多的训练后能让它进化到更好。
回到解释结构模型的层级图来。上蹿的哈斯图跟下跳的哈斯图刚好是一对生成的对立的（Adversarial）的拓扑层级网络。而这组对抗哈斯图有如下特点：
1、两者的层级数一样
2、每一层最少有一个要素在两个对抗图中的层级是一致的。这种要素称之为固定要素
3、在两个对抗图中，要素所属层级不同称之为活动要素
4、没有活动要素的一组哈斯图完全相同，即上蹿下跳哈斯图是同一个图
$$ Rank _{(j)}=\frac { Up_{(j)} + Down_{(j)} } 2 $$