层级划分
论文写作或者计算需要帮助可发邮件到 hwstu # sohu.com 把 #替换成@,请说清来意,不必拐弯抹角,浪费相互之间的时间。
返回首页
层级划分的计算有四个选项:
1、结果优先
2、原因优先
3、结果——原因轮换划分
4、原因——结果轮换划分
层级划分的前置知识
可达集合$R$,先行集合$Q$,共同集合$T$ 其中$T=R \bigcap Q$
在可达矩阵$R$中其要素$S1$的可达集合记作$R(S1)$。
在可达矩阵$R$中其要素$S1$的先行集合记作$Q(S1)$。
在可达矩阵$R$中其要素$S1$的共同集合记作$T(S1)$。
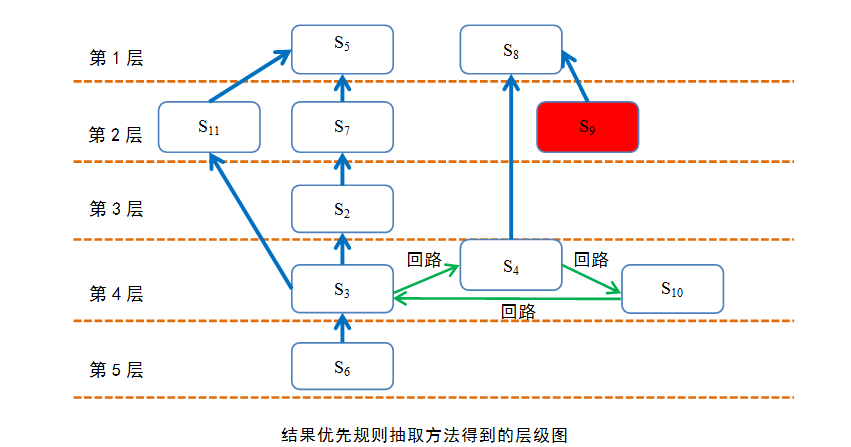
结果优先层级划分
某结果优先的层级划分如下
抽取规则:$ T(e_i)=R(e_i) $
这个是及其套路的方法,99%的用ISM方法的论文都是用这个经典的方法。也可以说是毫无新意的方法了。这种方法的本质就是先把系统中最终结果的要素抽取出来放到最上面一层。然后以此类推的抽取。
这种结果优先的层级抽取方法出来的层级图还有一个特征。
除了ISM层级图的三特征外,要素尽量放置在最上面的层级。
从物理学角度考虑,即重力势能最大。外形上看部分要素是上吊一样,悬着。头重脚轻。
可以取很多别名,上蹿型层级划分,上吊型层级划分,上位型层级划分,钉子型层级划分
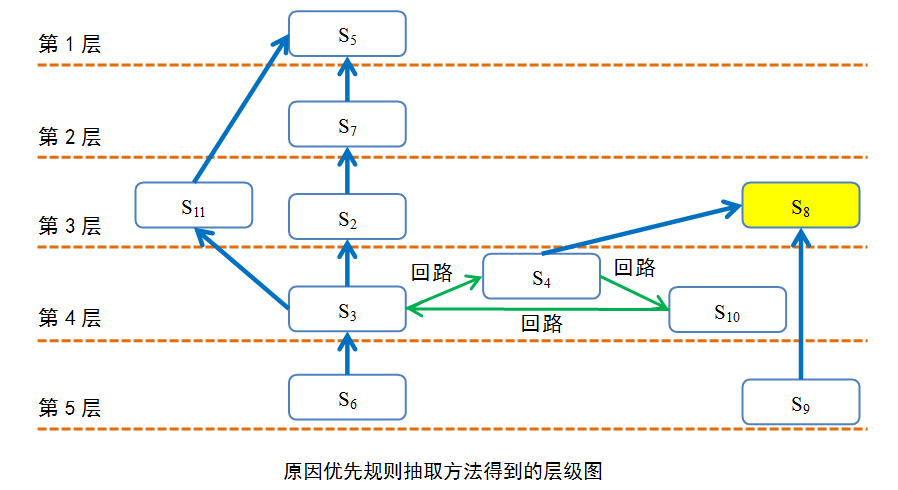
原因优先层级划分
某原因优先的层级划分如下
抽取规则:$ T(e_i)=Q(e_i) $
结果优先抽取是原命题的话,原因优先是逆命题。
这种原因优先的层级抽取方法出来的层级图还有一个特征。
除了ISM层级图三特征外,要素尽量放置在最下面的层级。
从物理学角度考虑,即重力势能最小。外形上看,就是底盘低,沉稳。
可以取很多别名,下跳型层级划分,蹲坑型层级划分,下位型层级划分
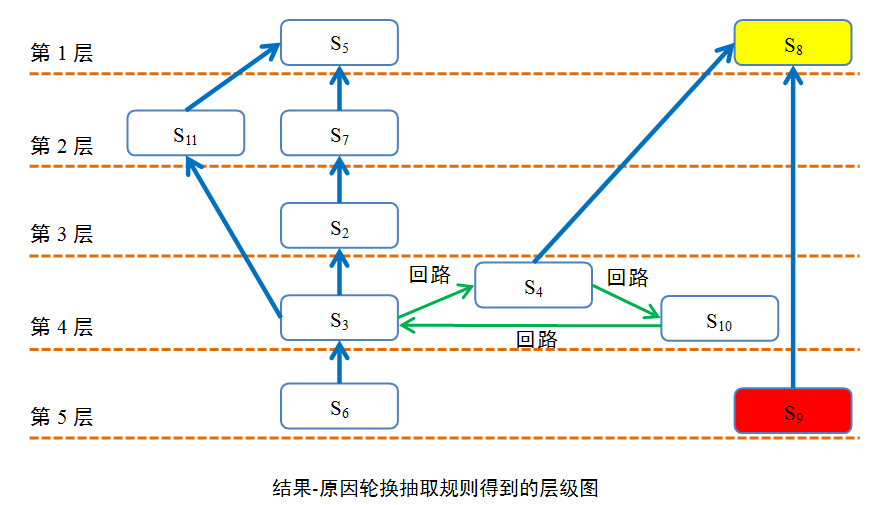
结果-原因轮换方式的层级划分
某最终层级图如下
结果-原因轮换法
即:第一次用,$T(e_i )=R(e_i)$ 第二次用$T(e_i )=Q(e_i)$ 其中结果优先抽取出的要素放置上层;原因优先抽取出的要素放置于下层。
除了ISM层级图三特征外,要素尽量放置在最上面与最下面的层级。即结果的要素尽量在上层,原因的要素尽量在下层。或者说输入尽量放下层,输出尽量放上层.
从物理学角度考虑,即弹性势能能最大。外形上看,就是拉得最开的弹簧。或者说哑铃,立着的哑铃型!
可以取别名,上蹿下跳层级划分法,结果原因轮番层级划分法,上下位轮换层级划分法,轮流坐庄法等等
原因——结果轮换方式的层级划分
某最终层级图如下
原因——结果轮换法
即:第一次用,$T(e_i )=Q(e_i)$ 第二次用$T(e_i )=R(e_i)$ 其中原因优先抽取出的要素放置于下层,结果优先抽取出的要素放置上层。
除了ISM层级图三特征外,要素尽量放置在最上面与最下面的层级。即结果的要素尽量在上层,原因的要素尽量在下层。或者说输入尽量放下层,输出尽量放上层.
从物理学角度考虑,即弹性势能能最大。外形上看,就是拉得最开的弹簧。或者说哑铃,立着的哑铃型!
可以取别名,下跳上蹿层级划分法,原因结果轮番层级划分法,下上位轮换层级划分法,轮流坐庄法等等
ISM层级拓扑图的三大特征
除了回路的箭头外,所有箭头朝向一致,通常是用向上来表示!这是一种习惯处理方式
回路中的要素,必定处于同一层级!
在符合上述规则的前提下,ISM抽取出来的层级数目最少!
推荐好玩的模型:扯蛋模型