阻尼解释结构模型

　　现实世界中，性质相反的两类属性是广泛存在的。即把模糊数的论域范围拓展到$[-1,1]$，在此论域范围内的解释结构模型称为阻尼解释结构模型。

$$ \begin{array} {c|c}{全称} & 英文全称& 简写 \\ \hline 不确定解释结构模型方法 &\color{red}{Uncertain \quad Interpretative \quad Structural \quad Modeling \quad Method} &\color{blue}{UISM} \\ \hline 阻尼解释结构模型方法 &\color{red}{Damp \quad Interpretative \quad Structural \quad Modeling \quad Method} &\color{blue}{DISM} \\ \hline 模糊解释结构模型方法 &\color{red}{Fuzzy \quad Interpretative \quad Structural \quad Modeling \quad Method} &\color{blue}{FISM} \\ \hline 解释结构模型方法 &\color{red}{Interpretative \quad Structural \quad Modeling \quad Method} &\color{blue}{ISM}\\ \hline \end{array} $$

　　上述四者的关系: $ \color{blue}{ISM \subset } \color{blue}{FISM \subset } \color{red}{DISM } \color{blue}{\subset } \color{blue}{UISM} $

因素的关系为$[-1,1]$模糊性

　　2003年，黄炜在其论文《黑客与反黑客思维研究的方法论启示——解释结构模型新探》中首次提出了阻尼解释结构模型。

　　其核心原则是把要素之间的关系进行了拓展，从论域$[0,1]$拓展到了$[-1,1]$。

　　即把模糊性扩展到负数的区间。现实中也存在着基于负数的关系判断。如一粒老鼠屎破坏一锅粥，成事不足败事有余。在科研中有存在着大量的以毒攻毒的思路。而这种关系称之为破坏性的、阻挠性的关系。

　　阻尼关系是使得原因要素，可达要素之间产生性质相左的影响。比如抗震救灾要素，对于地震损失就是关系为负！

　　对于一个有向图，可以用一个$n×n$矩阵来表示。n为系统要素的个数。矩阵的每一行和每一列对应图中一个节点（系统要素）。并规定，要素$e_i$对$e_j$有正影响时，矩阵元素$a_{ij}$为正数、其值为对应的权值；要素$e_i$对$e_j$有负影响时，矩阵元素$a_{ij}$为负数、其值为对应的权值，其中负的性质可以用不同的颜色加以区分,或者在有向边上标注数值加以区分；要素$e_i$对$e_j$无影响时，矩阵元素$a_{ij}$为0。

　　阻尼矩阵中取值描述如下：

$$ a_{ij}= \begin{cases} -x , \text{ $e_i$}\rightarrow \text{$e_j$ 有负影响} , x \in (0,1] \quad x的值为模糊测度值 \\ 0, \text{ $e_i$}\rightarrow \text{$e_j \quad \quad 无影响$} \\ +x, \text{ $e_i$}\rightarrow \text{$e_j$ 有正影响} , x \in (0,1] \quad x的值为模糊测度值 \end{cases} $$

　　　上述分段描述可简化为：$$ a_{ij}= x, \text{ $e_i$}\rightarrow \text{$e_j \quad \quad x \in$ [-1,+1]} \quad \quad x的值为模糊测度值 $$

　　模糊矩阵与阻尼矩阵：

　　阻尼矩阵是模糊矩阵的推广其核心是正负性质的表示

　　模糊矩阵的表达：$$ \require{AMScd} \begin{CD} X\\ @A \color{red}{-4}AA \\ Y\\ @A \color{blue}{5}AA\\ Z \end{CD} \Longleftrightarrow \begin{array} {c|c|c|c} {M_{3 \times 3}} & X & Y & Z \\ \hline X & 0 & 0 & 0 \\ \hline Y & \color{red}{-4} & 0 & 0 \\ \hline Z & 0 & \color{blue}{5} & 0 \\ \hline \end{array} \Longleftrightarrow \begin{array} {c|c|c|c} {M_{3 \times 3}} & X & Y & Z \\ \hline X & 0 & 0 & 0 \\ \hline Y & \color{blue}{0.8} & 0 & 0 \\ \hline Z & 0 & \color{blue}{1} & 0 \\ \hline \end{array} \Longleftrightarrow \begin{CD} X\\ @A A\color{blue}{0.8}A \\ Y\\ @A A \color{blue}{1}A\\ Z \end{CD} $$

　　阻尼矩阵的表达：$$ \require{AMScd} \begin{CD} X\\ @A \color{red}{-4}AA \\ Y\\ @A \color{blue}{5}AA\\ Z \end{CD} \Longleftrightarrow \begin{array} {c|c|c|c} {M_{3 \times 3}} & X & Y & Z \\ \hline X & 0 & 0 & 0 \\ \hline Y & \color{red}{-4} & 0 & 0 \\ \hline Z & 0 & \color{blue}{5} & 0 \\ \hline \end{array} \Longleftrightarrow \begin{array} {c|c|c|c} {M_{3 \times 3}} & X & Y & Z \\ \hline X & 0 & 0 & 0 \\ \hline Y & \color{red}{-0.8} & 0 & 0 \\ \hline Z & 0 & \color{blue}{1} & 0 \\ \hline \end{array} \Longleftrightarrow \begin{CD} X\\ @A A\color{red}{-0.8}A \\ Y\\ @A A \color{blue}{1}A\\ Z \end{CD} $$

阻尼算子

阻尼可达矩阵

　　设：原始阻尼矩阵$\tilde A$ 单位矩阵为$I$

　　$\tilde B=\tilde A +I$

　　当：$ \tilde B^{(k-1)}≠\tilde B^{k}=\tilde B^{(k+1)}= \tilde R$

　　$\tilde R$称为阻尼可达矩阵

　　$\tilde B$具有如下形式：

　　$$ \begin{array} {c|c|c|c|c|c|c|c}{ \tilde B_{n \times n}} &1 &2 &{\cdots} &n \\ \hline 1 & \color{blue}{1}&{b_{12}}&{\cdots}&{b_{1n}}\\ \hline 2 & {b_{21}}&\color{blue}{1}&{\cdots}&{b_{2n}}\\ \hline {\vdots} &{\vdots}&{\vdots}&\color{blue}{1}&{\vdots}\\ \hline n & {b_{n1}}&{b_{n2}}&{\cdots}&\color{blue}{1}\\ \hline \end{array} $$

　　设：$\tilde C = \tilde B \times \tilde B $

　　$ \tilde C=\left[ c_{ij} \right]_{n \times n} \quad \tilde B=\left[ b_{ij} \right]_{n \times n}$

　　$$ \begin{equation}\begin{split} c_{ij}&=\sum_{k=1}^n b_{ik}\odot b_{kj} \\ &=(b_{i1} \odot b_{1j}) \oplus (b_{i2} \odot b_{2j}) \oplus (b_{i3} \odot b_{3j}) \cdots \oplus \cdots(b_{in} \odot b_{nj})\\ \end{split}\end{equation} $$

　　其中$ \odot 为阻尼乘算子 $

　　其中$ \oplus 为阻尼加算子 $

　　对于任意$c_{ij}$不具有单调递增的特性，故阻尼可达矩阵不一定存在。当阻尼可达矩阵不存在时候，连乘下去具有周期的振荡性。

　　简单的判断可以如下方式进行，对于阻尼矩阵我们先取其极限来判断。很显然-1可以看成是一个矩阵值。对于$(-1)^k$来说不会出现确定值。它是在-1和1之间震荡。呈现有周期性。

　　DISM方法即Damp Interpretative Structural Modeling Method 中的Damp一词来自阻尼振动。把阻尼振动跟简谐振动合并在一起看，简谐振动就是阻尼振动的一个特例。把整个振动的过程看成求阻尼可达矩阵的过程，可以知道普通的阻尼振动会趋近于静止即处于阻尼可达矩阵的状态。而简谐振动则是一直呈现周期性的运动。即没有阻尼可达矩阵。

手性对称矩阵与手性拆分

　　手性对称矩阵： 手性一词来自于化学异构体的概念。即外形上看具有类似左手跟右手一样的镜面对称关系的立体几何体。

　　 $$ D=\begin{array} {c|c|c|c}{M_{3 \times3}} & A & B & C\\ \hline A &0 &\color{red}{-1} &0\\ \hline B &0 &0 &\color{blue}{1}\\ \hline C &0 &0 &0\\ \hline \end{array} $$

　　手性对称矩阵如下

　　$$ \begin{array} {c|ccc|ccc}{M_{6 \times6}} & +A &+B &+C &-A &-B &-C\\ \hline +A &0 &0 &0 &0 &\color{red}{1} &0\\ +B &0 &0 &\color{blue}{1} &0 &0 & 0\\ +C &0 &0 &0 &0 &0 &0\\ \hline -A &0 &\color{red}{1} &0 &0 &0 &0\\ -B &0 &0 &0 &0 &0 &\color{blue}{1}\\ -C &0 &0 &0 &0 &0 &0\\ \hline \end{array} $$

　　手性对称矩阵的特点

　　1、拓扑对称图，矩阵为沿着对角线的对称矩阵。

　　2、设任意两节点 $(v1,v2)$ 如果存在一个连通域点 $(+v1,-v1,+v2)$ 则 $(+v1,v1,+v2, -v2)$ 必定为同一个连通域。

　　推论1：有连通域 $(+v1,-v1,+v2,-v3,+v4,{\cdots} -vn)$则 $(+v1,-v1,+v2,-v2,+v3,-v3,+v4,-v4{\cdots} +vn,-vn)$ 必定为同一连通域

　　推论2：有连通域 $(-v1,+v2,-v3,+v4,{\cdots} -vn)$则 $(+v1,-v2,+v3,-v4{\cdots} +vn)$ 必定为另外一个镜像的连通域

　　手性拆分

　　从可能性上考虑，存在着保利不相容原理。保利不相容原理的基本描述为：同一轨道内的电子自旋方向相反。扩大该含义即一件事情发生了，必然对应着某件事情不发生。

　　因此对于连通域$(+v1,-v1,+v2,-v2,+v3,-v3,+v4,-v4{\cdots} +vn,-vn)$ 中任意成对节点${+vx,-vx}$只能取一个值。

　　取出的节点构成一个系统即为手性拆分矩阵。

$DISM \Longrightarrow ISM $　步骤

　　ISM中的矩阵对应的为布尔矩阵。即要把阻尼矩阵中的的值通过一系列转化变成布尔值，而该布尔矩阵最终得到为一个手性拆分后的矩阵。

　　方法一：

　　阻尼矩阵 $\tilde D$ 如下：

　　 $$ \tilde D=\begin{array} {c|c|c|c}{M_{3 \times3}} & a & b & c & d\\ \hline a &0 &\color{red}{-0.9} &0 &0\\ \hline b & \color{red}{-0.5}&0 &\color{blue}{0.8}&0\\ \hline c &0 &0 &0 &0\\ \hline d &0 &\color{blue}{0.9} &0 &0\\ \hline \end{array} $$

　　阻尼矩阵 $\tilde D$ 通常有取值的符号沿着对角线是对称的。值为0时看成任意的正负号。

　　阻尼矩阵 $\tilde D$ 转化成模糊矩阵 $\tilde F$ 可以取绝对值获得。

　　 $$ \tilde F=\begin{array} {c|c|c|c}{M_{3 \times3}} & a & b & c & d\\ \hline a &0 &\color{blue}{0.9} &0 &0\\ \hline b & \color{blue}{0.5}&0 &\color{blue}{0.8}&0\\ \hline c &0 &0 &0 &0\\ \hline d &0 &\color{blue}{0.9} &0 &0\\ \hline \end{array} $$

　　模糊矩阵 $\tilde F$ 选择对应的算子求出模糊可达矩阵 $\tilde R$

$$ \tilde R=\begin{array} {c|c|c}{M_{4 \times4}} &a &b &c &d\\ \hline a &1 &0.9 &0.8 &0\\ \hline b &0.5 &1 &0.8 &0\\ \hline c &0 &0 &1 &0\\ \hline d &0.5 &0.9 &0.8 &1\\ \hline \end{array} $$ $$ 阈值集合\ddot \Delta = (0.5, 0.8, 0.9, 1) $$

　　由阈值集合对模糊可达矩阵 $\tilde R$ 得到截距阵的骨架矩阵并求出层级图。

　　截距 $\lambda$ = 0.5 得如下矩阵

$$R_{0.5} =\begin{array} {c|c|c}{M_{4 \times4}} &a &b &c &d\\ \hline a &1 &1 &1 &0\\ \hline b &1 &1 &1 &0\\ \hline c &0 &0 &1 &0\\ \hline d &1 &1 &1 &1\\ \hline \end{array} \Longrightarrow S_{0.5}=\begin{array} {c|c|c|c|c|c|c|c}{M_{4 \times4}} &a &b &c &d\\ \hline a &0 &1 &0 &0\\ \hline b &1 &0 &1 &0\\ \hline c &0 &0 &0 &0\\ \hline d &1 &0 &0 &0\\ \hline \end{array} \Longrightarrow 骨架矩阵S_{0.5}=\begin{array} {c|c|c|c|c|c|c|c}{M_{3 \times 3}} &a +b &c &d\\ \hline a+b &0 &1 &0 \\ \hline c &0 &0 &0 \\ \hline d &1 &0 &0 \\ \hline \end{array} $$

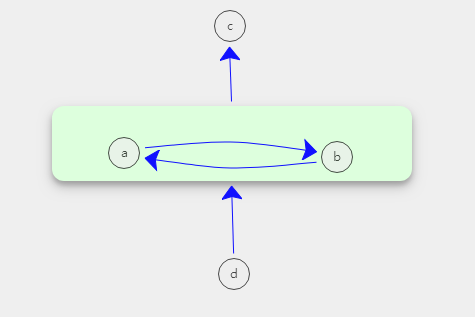
　　上述即为ISM的层级图框架。

　　对于要素的正负需要从原因要素即下层要素给出初始判断，根据性质层层往上计算得出。具体计算请看方法二。

　　方法二：

　　阻尼矩阵 $\tilde D$ 如下：

　　阻尼矩阵 $\tilde D$ 转化成手性对称的模糊矩阵 $ \tilde Fhand $

　 $$ \tilde f_{ij}= \begin{cases} \tilde f_{(-i)(+j)}=|\tilde d_{ij}| 且 \tilde f_{(+i)(-j)}=|\tilde d_{ij}| , \tilde d_{ij}< 0 \\ \tilde f_{(-i)(-j)}=|\tilde d_{ij}| 且 \tilde f_{(+i)(+j)}=|\tilde d_{ij}| , \tilde d_{ij}> 0 \end{cases} $$

　　$$ \tilde Fhand = \begin{array} {c|cccc|cccc}{M_{8 \times8}} & +a &+b &+c &+d &-a &-b &-c &-d\\ \hline +a &0 &0 &0 &0 &0 &0.9 &0 &0 \\ +b &0 &0 &0.8 &0 &0.5 &0 &0 &0 \\ +c &0 &0 &0 &0 &0 &0 &0 &0\\ +d &0 &0.9 &0 &0 &0 &0 &0 &0\\ \hline -a &0 &0.9 &0 &0 &0 &0 &0 &0 \\ -b &0.5 &0 &0 &0 &0 &0 &0.8 &0 \\ -c &0 &0 &0 &0 &0 &0 &0 &0\\ -d &0 &0 &0 &0 &0 &0.9 &0 &0\\ \hline \end{array} $$

　　上述矩阵为模糊矩阵，根据FISM方法求出如下结构截距 $\lambda$ = 0.5

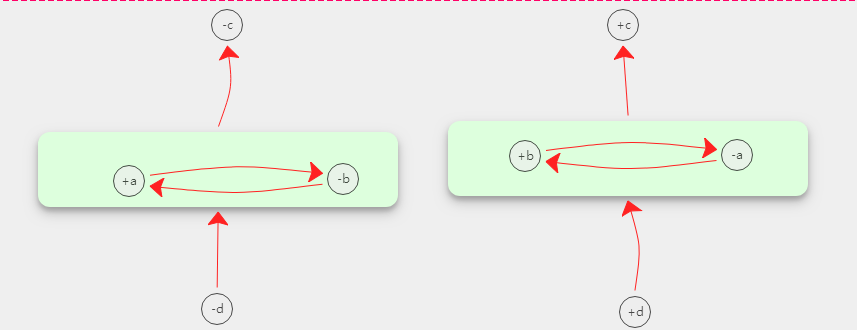
　　截距 $\lambda$ = 0.8

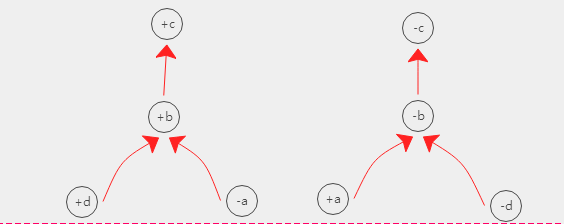
　　截距 $\lambda$ = 0.9

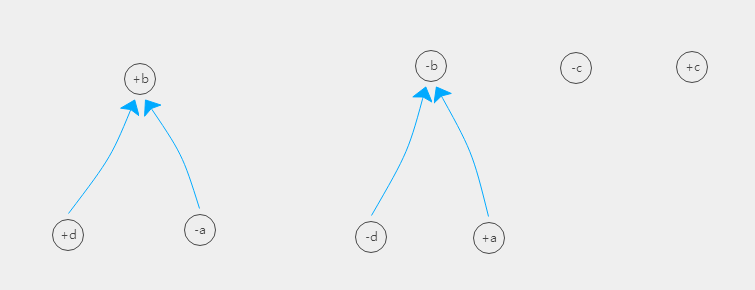
DISM讨论

　　DISM的推荐如下：

$$ \require{cancel} \require{AMScd} \begin{CD} \tilde D=\left[ \tilde d_{ij} \right]_\color{blue}{n \times n}@>对称平移>> \tilde Fhand=\left[ \tilde f_{ij} \right]_\color{red}{2n \times 2n}@>截距阵>>R_{\lambda}=\left[ r_{ij} \right]_\color{red}{2n \times 2n}@>ISM方法>>最简层次化的菊花链@>如果层次图为未拆分手性图按照层级从下往下拆分>>ISM层级图 \\ \end{CD} $$

　　讨论

　　1、正负号的含义

　　在阻尼矩阵的值中存在着正负号，同时在手性矩阵要素的标识中存在。两者的关系如下图所表示。

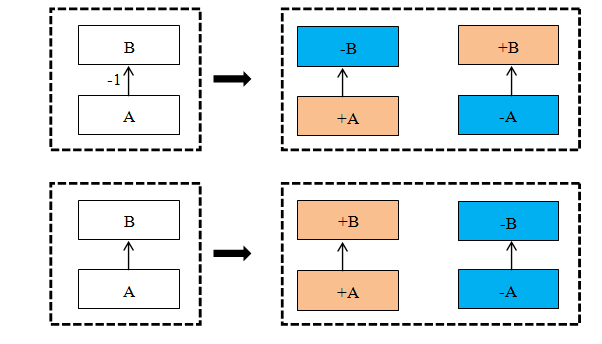
　　2、要素含义的解读

　　如下图，由食物链推导出的ISM

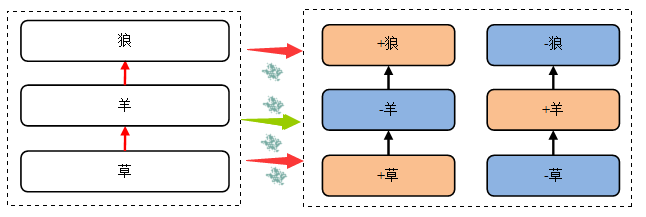
　　以狼为例：左边结构图中狼是名词，代表一种动物。而右边的+狼与-狼是狼的一种属性，含义是某时刻狼的数量变化的方向。

　　左图为食物链的ISM层级图。

　　右图为物种数量变化方向的ISM层级图。它是一个对称的两个不连通图组成。

　　3、对于没有拆分的结构，进行拆分时候，由下往上逐步进行