对抗解释结构模型(AISM)在线计算

论文写作或者计算需要帮助可发邮件到 hwstu # sohu.com 把 #替换成@，请说清来意，不必拐弯抹角，浪费相互之间的时间。
目前暂时限制到8个要素的输入，输入更多要素需付费。

返回首页

付费后取消要素数目的限制。点下面的＋号后不再是灰色，可自行运算

$$ \require{cancel} \require{AMScd} \begin{CD} 点击＋号 @>> >增加要素数目 @>> > 输入关系矩阵（对角线不用输入） @>>> 点计算，即列出所有过程与结果。@>>>层级拓扑图可以拖拽 \\ \end{CD} $$

点击计算按钮后会自动运算，并记录每个过程，并绘制可以拖拽的拓扑层次图（俗称扯蛋模型） 。

流程图与说明如下


你没有输入参数，本处随机给出一个


本系统基本信息为

$$A=\begin{array} {c|c|c|c|c|c|c|c}{M_{8 \times8}} &A1 &A2 &A3 &A4 &A5 &A6 &A7 &A8\\ \hline A1 & &1 & & & & & & \\ \hline A2 &1 & & &1 & & & & \\ \hline A3 & &1 & & & & & & \\ \hline A4 & &1 & & & & & & \\ \hline A5 & & & & & & &1 & \\ \hline A6 & & & & & & &1 &1\\ \hline A7 & & &1 & & & & & \\ \hline A8 & & & & & & & & \\ \hline \end{array} $$

论文范本——要素关系为优劣关系，好坏关系：基于对抗解释结构模型的军事训练方法可推广性评价模型

论文范本——要素关系为因果关系：Research on the Influencing Factors of Kite Culture Inheritance Based on an Adversarial Interpretive Structure Modeling Method

论文范本——要素关系为优劣比较关系：基于对抗解释结构模型方法的沿海智慧港口竞争力研究_谢希霖

论文范本——要素关系为因果关系：基于Probit-AISM模型的生态农业采纳行为分析_魏雪

论文范本——要素关系为因果关系：基于AISM的水利工程项目治理影响因素研究_赵贤晨

论文范本——要素关系为因果关系：基于DEMATEL-AISM法的的装配式建筑预制构件成本影响因素分析_魏宏亮

论文范本——要素关系为优劣比较关系：中国东部省份科技创新能力综合评价 ——基于TOPSIS-AISM模型

原始关系矩阵：

$$A=\begin{array} {c|c|c|c|c|c|c|c}{M_{8 \times8}} &A1 &A2 &A3 &A4 &A5 &A6 &A7 &A8\\ \hline A1 & &1 & & & & & & \\ \hline A2 &1 & & &1 & & & & \\ \hline A3 & &1 & & & & & & \\ \hline A4 & &1 & & & & & & \\ \hline A5 & & & & & & &1 & \\ \hline A6 & & & & & & &1 &1\\ \hline A7 & & &1 & & & & & \\ \hline A8 & & & & & & & & \\ \hline \end{array} $$

邻接相乘矩阵为：

$$B=\begin{array} {c|c|c|c|c|c|c|c}{M_{8 \times8}} &A1 &A2 &A3 &A4 &A5 &A6 &A7 &A8\\ \hline A1 &1 &1 & & & & & & \\ \hline A2 &1 &1 & &1 & & & & \\ \hline A3 & &1 &1 & & & & & \\ \hline A4 & &1 & &1 & & & & \\ \hline A5 & & & & &1 & &1 & \\ \hline A6 & & & & & &1 &1 &1\\ \hline A7 & & &1 & & & &1 & \\ \hline A8 & & & & & & & &1\\ \hline \end{array} $$

可达矩阵为：

$$R=\begin{array} {c|c|c|c|c|c|c|c}{M_{8 \times8}} &A1 &A2 &A3 &A4 &A5 &A6 &A7 &A8\\ \hline A1 &1 &1 & &1 & & & & \\ \hline A2 &1 &1 & &1 & & & & \\ \hline A3 &1 &1 &1 &1 & & & & \\ \hline A4 &1 &1 & &1 & & & & \\ \hline A5 &1 &1 &1 &1 &1 & &1 & \\ \hline A6 &1 &1 &1 &1 & &1 &1 &1\\ \hline A7 &1 &1 &1 &1 & & &1 & \\ \hline A8 & & & & & & & &1\\ \hline \end{array} $$

绘制图表

这玩意就是凑数字的，其中可达矩阵行为1的总数称之为驱动力也称之为原因度，原因的含量。 某要素列为1的总数称之为依赖数，结果数。
里面的矩阵，选中右键选择TeX 格式可以在word里的公式编辑器里直接编辑矩阵，但是不好看，建议直接用表格格式存矩阵。
点击右键，会有惊喜，可以把图片存在本地，也可以自己拷贝到微信等发给别人。

抽取的过程如下

结果优先——UP型抽取过程 原因优先——DOWN型抽取过程
$$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline A1&\color{red}{\fbox{A1,A2,A4}}&\color{red}{\fbox{A1,A2,A4}} \\\hline A2&\color{red}{\fbox{A1,A2,A4}}&\color{red}{\fbox{A1,A2,A4}} \\\hline A3&A1,A2,A3,A4&A3 \\\hline A4&\color{red}{\fbox{A1,A2,A4}}&\color{red}{\fbox{A1,A2,A4}} \\\hline A5&A1,A2,A3,A4,A5,A7&A5 \\\hline A6&A1,A2,A3,A4,A6,A7,A8&A6 \\\hline A7&A1,A2,A3,A4,A7&A7 \\\hline A8&\color{red}{\fbox{A8}}&\color{red}{\fbox{A8}} \\\hline \end{array} $$ $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline A1&A1,A2,A3,A4,A5,A6,A7&A1,A2,A4 \\\hline A2&A1,A2,A3,A4,A5,A6,A7&A1,A2,A4 \\\hline A3&A3,A5,A6,A7&A3 \\\hline A4&A1,A2,A3,A4,A5,A6,A7&A1,A2,A4 \\\hline A5&\color{blue}{\fbox{A5}}&\color{blue}{\fbox{A5}} \\\hline A6&\color{blue}{\fbox{A6}}&\color{blue}{\fbox{A6}} \\\hline A7&A5,A6,A7&A7 \\\hline A8&A6,A8&A8 \\\hline \end{array} $$
抽取出A1、A2、A4、A8放置上层，删除后剩余的情况如下 抽取出A5,A6放置下层，删除后剩余的情况如下
$$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline A3&\color{red}{\fbox{A3}}&\color{red}{\fbox{A3}} \\\hline A5&A3,A5,A7&A5 \\\hline A6&A3,A6,A7&A6 \\\hline A7&A3,A7&A7 \\\hline \end{array} $$ $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline A1&A1,A2,A3,A4,A7&A1,A2,A4 \\\hline A2&A1,A2,A3,A4,A7&A1,A2,A4 \\\hline A3&A3,A7&A3 \\\hline A4&A1,A2,A3,A4,A7&A1,A2,A4 \\\hline A7&\color{blue}{\fbox{A7}}&\color{blue}{\fbox{A7}} \\\hline A8&\color{blue}{\fbox{A8}}&\color{blue}{\fbox{A8}} \\\hline \end{array} $$
抽取出A3放置上层，删除后剩余的情况如下 抽取出A7,A8放置下层，删除后剩余的情况如下
$$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline A5&A5,A7&A5 \\\hline A6&A6,A7&A6 \\\hline A7&\color{red}{\fbox{A7}}&\color{red}{\fbox{A7}} \\\hline \end{array} $$ $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline A1&A1,A2,A3,A4&A1,A2,A4 \\\hline A2&A1,A2,A3,A4&A1,A2,A4 \\\hline A3&\color{blue}{\fbox{A3}}&\color{blue}{\fbox{A3}} \\\hline A4&A1,A2,A3,A4&A1,A2,A4 \\\hline \end{array} $$
抽取出A7放置上层，删除后剩余的情况如下 抽取出A3放置下层，删除后剩余的情况如下
$$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline A5&\color{red}{\fbox{A5}}&\color{red}{\fbox{A5}} \\\hline A6&\color{red}{\fbox{A6}}&\color{red}{\fbox{A6}} \\\hline \end{array} $$ $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline A1&\color{blue}{\fbox{A1,A2,A4}}&\color{blue}{\fbox{A1,A2,A4}} \\\hline A2&\color{blue}{\fbox{A1,A2,A4}}&\color{blue}{\fbox{A1,A2,A4}} \\\hline A4&\color{blue}{\fbox{A1,A2,A4}}&\color{blue}{\fbox{A1,A2,A4}} \\\hline \end{array} $$
抽取出A5、A6放置上层，删除后剩余的情况如下 抽取出A1,A2,A4放置下层，删除后剩余的情况如下

抽取方式的结果如下

层级 结果优先——UP型 原因优先——DOWN型
第0层 A1,A2,A4,A8 A1,A2,A4
第1层 A3 A3
第2层 A7 A7,A8
第3层 A5,A6 A5,A6

一般性骨架矩阵

求解过程如链接所示：缩点、缩边,再把回路要素替代回去。这步是最难的，本处用的算法那人得了计算机界的诺奖-图领奖，算法为trajan算法的组合。现在的论文都忽略了这步。

计算一般性骨架矩阵 \begin{CD} R @>缩点运算>>R' @>缩边运算>>S' @>以最简菊花链表示回路>>S \ \end{CD}

可达矩阵 $R$的缩点矩阵 $R'$

$$R'=\begin{array} {c|c|c|c|c|c|c|c}{M_{6 \times6}} &A1＋A2＋A4 &A3 &A5 &A6 &A7 &A8\\ \hline A1＋A2＋A4 &1 & & & & & \\ \hline A3 &1 &1 & & & & \\ \hline A5 &1 &1 &1 & &1 & \\ \hline A6 &1 &1 & &1 &1 &1\\ \hline A7 &1 &1 & & &1 & \\ \hline A8 & & & & & &1\\ \hline \end{array} $$

缩点矩阵 $R'$的缩边矩阵 $S'$

$$S'=\begin{array} {c|c|c|c|c|c|c|c}{M_{6 \times6}} &A1＋A2＋A4 &A3 &A5 &A6 &A7 &A8\\ \hline A1＋A2＋A4 & & & & & & \\ \hline A3 &1 & & & & & \\ \hline A5 & & & & &1 & \\ \hline A6 & & & & &1 &1\\ \hline A7 & &1 & & & & \\ \hline A8 & & & & & & \\ \hline \end{array} $$

以最简菊花链表示回路的一般性骨架矩阵 $S$

$$S=\begin{array} {c|c|c|c|c|c|c|c}{M_{8 \times8}} &A1 &A2 &A3 &A4 &A5 &A6 &A7 &A8\\ \hline A1 & &1 & & & & & & \\ \hline A2 & & & &1 & & & & \\ \hline A3 & &1 & & & & & & \\ \hline A4 &1 & & & & & & & \\ \hline A5 & & & & & & &1 & \\ \hline A6 & & & & & & &1 &1\\ \hline A7 & & &1 & & & & & \\ \hline A8 & & & & & & & & \\ \hline \end{array} $$

一组对抗层级拓扑图即{UP|DOWN}的原因到结果的系列层级图

对要素可以拖拽（扯蛋），尽量减少线的交叉。但是不要改变要素所在的层级，即扯蛋最好是横向的扯蛋。

UP型菊花链，即结果优先的有向拓扑层级图

　　第0层
　　第1层
　　第2层
　　第3层
A1
A2
A4
A3
A7
A5
A8
A6

DOWN型菊花链，即原因优先的有向拓扑层级图

　　第0层
　　第1层
　　第2层
　　第3层
A1
A2
A4
A3
A7
A5
A8
A6

流程图-竖版

流程图-横版

画法的要点:

第一非活动要素位置尽量不变

活动要素（用色块以示区别）

变化的位置最好显示在同一侧。

一组拓扑图并排绘制，这样活动要素一目了然，吸引关注

箭头不要拐弯，但是要尽量减少交叉。

两篇范文的简单点评

1：基于对抗解释结构模型的军事训练方法可推广性评价模型

是好坏比较型

2：Research on the Influencing Factors of Kite Culture Inheritance Based on an AISM

是常规的因果型

论文2中有一处错误$\{S1, S13 \}∩ \{S1, S13 \} = \{S1, S13\}$其中的交集运算是错的，应该是并集。这种就是三个因果层次的划分依据。

论文2 是英文写作，相关的术语可以参考，如骨架矩阵的英文单词，拓扑层级图的英文等等。

常见的四个几个定义如下：

Adversarial Interpretive Structure Modeling Method（简称 AISM）是在经典的解释结构模型（ISM）基础上，融入生成对抗网络（GAN）中的博弈对抗（Adversarial）思想，最新提出的一种模型方法。一言以蔽之AISM就是在不损失系统功能的前提下，通过相反的层级抽取规则，得出一对最简的层次化的拓扑图。

活动要素（Activity elements） 在对抗有向拓扑层级图中处于不同的层级的要素。

可拓变系统（Extension variable system），也叫活动系统或拓扑活动系统 具有活动要素的系统。

刚性系统（Rigid system），也叫拓扑刚性系统（Topological rigid system） 不含有活动要素的系统。

完全刚性系统（Completely rigid system）： 完全刚性系统具有如下三个特性：

其一，关系矩阵中的要素从小到大排序后形成上三角矩阵的满阵形式，即对角线右上方全为1，对角线左下方全为0；同理，关系矩阵中的要素从大到小排列后，则形成下三角矩阵的满阵形式。

其二，两种有向拓扑层级图的结果是一致的，展现为直链型。（一条棍子）

其三，任意两个评价对象（样本，要素，方案）之间都有确定的比较关系（优劣，好坏，可达，大小）。

超级完全刚性系统（Super Completely rigid system）： 比完全刚性系统多一个属性

一条棍子的某个节点含有一个回路系统

绘图例子与说明

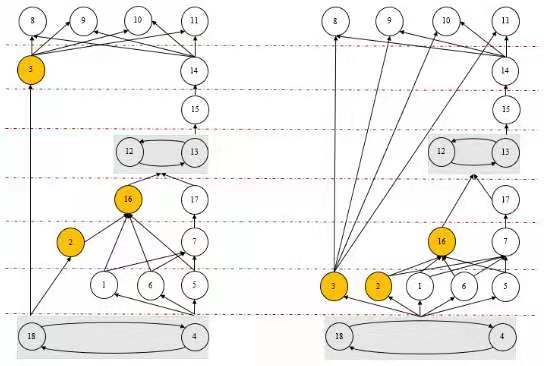
固定要素 在两个对立图中的位置是一模一样的。不动弹的！

活动要素 用深色标出，这样人的目光与注意力一下就集中在了深色要素上

回路相关的箭头 指向回路的有向边，只到边框即可，发出的从边框发出即可。

不足的部分

层级数通常从上到下增加，如最上层设置为L0

层级的因果关系与优劣关系在两张图的边上分别画一个由最下层到最上层的一个箭头，最上层写结果，发出端写原因；如果是优劣关系，上面写优，下面写劣；如果是好坏关系，上面写好，下面写差。总之关系的性质要写明。

意义等该如何吹水，以因果关系为例

一、从UP与DOWN的层级拓扑来看存在着活动要素 巴拉巴拉巴拉……所以它是一个活动系统（可变态系统）

二、回路分析 很显然上图有两个回路，这两个回路可以当成一个要素（子系统）处理，巴拉巴拉

三、因果层级分析

UP型 $ …… \prec \{ (12,13)\} …… \prec……\prec\{3,14 \} \prec \{8,9,10,11 \}$

$ \prec $ 这个符号要能从word里找到，是装逼利器，是规范化的表述。可以念成牛逼于，结果，可达，

四、三个世界划分理论 根本结果最终结果的要素（最上层求并集）； 根本原因要素（最下层两边求并集，即多的一个）；中间要素，其它的

如需用到其它方法如：扯蛋模型
可发邮件到 hwstu # sohu.com 把 #替换成@